Predicting Hospital Readmission with a Binary Classification Model¶
In this tutorial, we’ll be looking at hospital admission data in patients with diabetes. This dataset was collected from 130 hospitals in the United States from 1999 to 2008. More details can be found on the UCI Machine Learning Repository website.
This walkthrough is divided into two parts:
- Data preprocessing (Steps 1-5), which involves data cleaning, exploration, and feature engineering
- Data modelling (Steps 6-10), where we will train a machine learning model to predict whether a patient will be readmitted to the hospital
Data Preprocessing¶
Step 1: Importing Depedencies¶
Before getting started, we’ll need to import several packages. These include:
- pandas - a package for performing data analysis and manipulation
- numpy - a package for scientific computing
- matplotlib - the standard Python plotting package
- seaborn - a dataframe-centric visualization package that is built off of matplotlib
In [2]:
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
Step 2: Load the Data¶
We will be loading in the data as a pandas.DataFrame.
The data is stored in a csv file, which we can access locally (see
data/patient_data.csv) or in the cloud (stored in a AWS S3 bucket).
We’ll import the S3 version of this data using a pandas method called
read_csv.
In [3]:
data = pd.read_csv("https://s3.us-east-2.amazonaws.com/explore.datasets/diabetes/patient_data.csv")
To get a glimpse of our data, we can use either the head(), which
shows the first 5 rows of the dataframe.
In [4]:
data.head()
Out[4]:
| encounter_id | patient_nbr | race | gender | age | weight | admission_type_id | discharge_disposition_id | time_in_hospital | medical_specialty | ... | examide | citoglipton | insulin | glyburide-metformin | glipizide-metformin | glimepiride-pioglitazone | metformin-rosiglitazone | metformin-pioglitazone | diabetesMed | readmitted | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2278392 | 8222157 | Caucasian | Female | [0-10) | NaN | 6 | 25 | 1 | Pediatrics-Endocrinology | ... | No | No | No | No | No | No | No | No | No | NO |
| 1 | 149190 | 55629189 | Caucasian | Female | [10-20) | NaN | 1 | 1 | 3 | NaN | ... | No | No | Up | No | No | No | No | No | Yes | >30 |
| 2 | 64410 | 86047875 | AfricanAmerican | Female | [20-30) | NaN | 1 | 1 | 2 | NaN | ... | No | No | No | No | No | No | No | No | Yes | NO |
| 3 | 500364 | 82442376 | Caucasian | Male | [30-40) | NaN | 1 | 1 | 2 | NaN | ... | No | No | Up | No | No | No | No | No | Yes | NO |
| 4 | 16680 | 42519267 | Caucasian | Male | [40-50) | NaN | 1 | 1 | 1 | NaN | ... | No | No | Steady | No | No | No | No | No | Yes | NO |
5 rows × 44 columns
How many rows and columns are in our dataset?¶
In [5]:
data.shape
Out[5]:
(101766, 44)
Our dataset has 101,766 rows and 45 columns. Each row represents a
unique hospital admission. Columns represent patient demographics,
medical details, and admission-specific information such as length of
stay (time_in_hospital). We can see a list of all columns by
applying .columns to our dataframe.
In [6]:
print(f"Columns: {data.columns.tolist()}")
Columns: ['encounter_id', 'patient_nbr', 'race', 'gender', 'age', 'weight', 'admission_type_id', 'discharge_disposition_id', 'time_in_hospital', 'medical_specialty', 'num_lab_procedures', 'num_procedures', 'num_medications', 'number_outpatient', 'number_emergency', 'number_inpatient', 'number_diagnoses', 'max_glu_serum', 'A1Cresult', 'metformin', 'repaglinide', 'nateglinide', 'chlorpropamide', 'glimepiride', 'acetohexamide', 'glipizide', 'glyburide', 'tolbutamide', 'pioglitazone', 'rosiglitazone', 'acarbose', 'miglitol', 'troglitazone', 'tolazamide', 'examide', 'citoglipton', 'insulin', 'glyburide-metformin', 'glipizide-metformin', 'glimepiride-pioglitazone', 'metformin-rosiglitazone', 'metformin-pioglitazone', 'diabetesMed', 'readmitted']
Looking at the columns, we can see that a large proportion are medication names. Let’s store these column names as a separate list, which we’ll get back to in a bit.
In [7]:
medications = ['metformin', 'repaglinide', 'nateglinide', 'chlorpropamide', 'glimepiride',
'acetohexamide', 'glipizide', 'glyburide', 'tolbutamide', 'pioglitazone',
'rosiglitazone', 'acarbose', 'miglitol', 'troglitazone', 'tolazamide',
'examide', 'citoglipton', 'insulin', 'glyburide-metformin', 'glipizide-metformin',
'glimepiride-pioglitazone', 'metformin-rosiglitazone', 'metformin-pioglitazone']
print(f"There are {len(medications)} medications represented as columns in the dataset.")
There are 23 medications represented as columns in the dataset.
How many hospital admissions and unique patients are in the dataset?¶
In [8]:
n_admissions = data['encounter_id'].nunique()
n_patients = data['patient_nbr'].nunique()
print(f"Number of hospital admissions: {n_admissions:,}")
print(f"Number of unique patients: {n_patients:,}")
Number of hospital admissions: 101,766
Number of unique patients: 71,518
How many patients have had more than one hospital admission?¶
In [9]:
admissions_per_patient = data['patient_nbr'].value_counts().reset_index()
admissions_per_patient.columns = ['patient_nbr', 'count']
multiple_admissions = admissions_per_patient[admissions_per_patient['count'] > 1]
In [10]:
print(f"Proportion of patients that have multiple admissions: {multiple_admissions['patient_nbr'].nunique()/n_patients:.2%}")
print(f"Maximum number of admissions for a given patient: {multiple_admissions['count'].max()}")
Proportion of patients that have multiple admissions: 23.45%
Maximum number of admissions for a given patient: 40
Almost one-quarter of the patients (23.45%) have had more than 1 hosptial admission. The maximum number of hospital admissions for a given patient is 40.
Step 3: Data Cleaning¶
Data cleaning is a crucial step in the machine learning pipeline, and typically requires the most time and effort in any data science project.
Decoding Admission Type¶
The admission_type_id column describes the type of admission and is
represented by integers. The id column links to descriptors found in
a separate file. We’ll update this column so that it represents the
descriptor name instead of simply the id number.
Our mapper files are located in data/id_mappers/. They are also
stored on the cloud in a AWS S3 bucket.
In [11]:
admission_type = pd.read_csv("https://s3.us-east-2.amazonaws.com/explore.datasets/diabetes/id_mappers/admission_type_id.csv")
admission_type
Out[11]:
| admission_type_id | description | |
|---|---|---|
| 0 | 1 | Emergency |
| 1 | 2 | Urgent |
| 2 | 3 | Elective |
| 3 | 4 | Newborn |
| 4 | 5 | Not Available |
| 5 | 6 | NaN |
| 6 | 7 | Trauma Center |
| 7 | 8 | Not Mapped |
We can see that the admission type mapper file has 3 values which represent missing data:
- NaN
- ‘Not Mapped’
- ‘Not Available’
Let’s collapse these into one category that represents a missing value.
We can use pandas
replace
method to do this.
In [12]:
missing_values = ['nan', 'Not Available', 'Not Mapped']
admission_type['description'] = admission_type['description'].replace(missing_values, np.nan)
In [13]:
admission_type.columns = ['admission_type_id', 'admission_type']
In [14]:
data = data.merge(admission_type, on='admission_type_id')
Now that we have a “clean” mapper, we can apply it to our dataset. We
can
map
admission_type_id values in our original dataframe to the
descriptors in our admission_type_mapper dictionary.
In [15]:
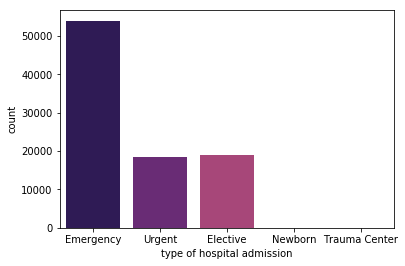
data['admission_type'].value_counts()
Out[15]:
Emergency 53990
Elective 18869
Urgent 18480
Trauma Center 21
Newborn 10
Name: admission_type, dtype: int64
In [16]:
sns.countplot(x='admission_type', data=data, palette='magma')
plt.xlabel('type of hospital admission')
plt.show()
Decoding Discharge Location¶
In [17]:
discharge_disposition = pd.read_csv("https://s3.us-east-2.amazonaws.com/explore.datasets/diabetes/id_mappers/discharge_disposition_id.csv")
discharge_disposition.sample(n=5, random_state=416)
Out[17]:
| discharge_disposition_id | description | |
|---|---|---|
| 13 | 14 | Hospice / medical facility |
| 8 | 9 | Admitted as an inpatient to this hospital |
| 14 | 15 | Discharged/transferred within this institution... |
| 20 | 21 | Expired, place unknown. Medicaid only, hospice. |
| 29 | 29 | Discharged/transferred to a Critical Access Ho... |
In medicine, “expired” is a term that describes a patient who has died. We only want to predict hospital readmission for living patients so we’re going to remove hospital admissions in which the patient was recorded as “expired” upon being discharged in our dataset.
We’ll first convert our description column to lowercase
(str.lower()), then we’ll search for rows that contain “expired”
(str.contains("expired")).
In [18]:
discharge_disposition['expired'] = discharge_disposition['description'].str.lower().str.contains('expired')
Now let’s take a look at all discharge dispositions that indicate an expired patient. We’ll create a new dataframe that filters for rows in which the expired column is True.
In [19]:
discharge_expired = discharge_disposition[discharge_disposition['expired']==True]
discharge_expired
Out[19]:
| discharge_disposition_id | description | expired | |
|---|---|---|---|
| 10 | 11 | Expired | True |
| 18 | 19 | Expired at home. Medicaid only, hospice. | True |
| 19 | 20 | Expired in a medical facility. Medicaid only, ... | True |
| 20 | 21 | Expired, place unknown. Medicaid only, hospice. | True |
In [20]:
expired_ids = discharge_expired['discharge_disposition_id'].tolist()
print(f"discharge_disposition_id's that indicate an expired patient: {expired_ids}")
discharge_disposition_id's that indicate an expired patient: [11, 19, 20, 21]
The next step is to remove all rows in our original dataset that has
discharge_disposition_id equal to one of the values in our
expired_ids list.
In [21]:
data = data[~data['discharge_disposition_id'].isin(expired_ids)]
After removing expired patients, how many patients do we have in our dataset?
In [22]:
n_patients_nonexpired = data['patient_nbr'].nunique()
print(f"Original number of patients: {n_patients:,}")
print(f"Number of expired patients: {n_patients-n_patients_nonexpired:,}")
print(f"After filtering out expired patients: {n_patients_nonexpired:,}")
Original number of patients: 71,518
Number of expired patients: 1,079
After filtering out expired patients: 70,439
We had 1,079 expired patients in our dataset. After removing them, our dataset has 70,439 patients.
Converting Medication Features From Categorical to Boolean¶
Remember that list of medications we created when we loaded our data in Step 2? We’re going to convert these medication columns into boolean variables.
In [23]:
data[medications[0]].value_counts()
Out[23]:
No 80216
Steady 18256
Up 1067
Down 575
Name: metformin, dtype: int64
Medication columns are currently categorical datatypes that have several possible categories including:
- “No” (not taking the medication)
- “Up” (increased medication dose)
- “Down” (decrease medication dose)
- “Steady” (no changes in dose)
To keep things simple, we’ll update the column to “0” (not taking the medication) to “1” (taking the medication). We’re losing out on information regarding their dose change, but it’s a compromise we’re willing to make in order to simplify our dataset.
We can use
numpy.where
to convert all instances of “No” to 0 and everything else (i.e.,
“Up”, “Down”, “Steady”) to 1. Let’s loop through all medications and
convert each column to boolean.
In [24]:
for m in medications:
data[f'{m}_bool'] = np.where(data[m]=='No', 0, 1)
data = data.drop(columns=m)
Our medication data are now represented as boolean features. Let’s take a look at the prevalence of these medications. We’ll calcualte the proportion of patients taking each type of medication. Because some patients have had multiple hospital admissions in this dataset, we’ll need to do some wrangling to determine whether a patient was on a given medication during any of their admissions. The wrangling process consists of the following steps:
- applying
groupbytopatient_nbrand calculate the sum of admissions in which the patient was administered a medication - convert the column to boolean such that patients that have “0” are False and “1” is True
- calculate the sum of patients on that specific medication
- calculate the proportion of patients who were administered that medication
In [25]:
prevalence = []
for m in medications:
patient_meds = data.groupby('patient_nbr')[f'{m}_bool'].sum().reset_index()
patient_meds[f'{m}_bool'] = patient_meds[f'{m}_bool'].astype(bool)
n_patients_on_med = patient_meds[f'{m}_bool'].sum()
proportion = n_patients_on_med/n_patients
prevalence.append(proportion)
Now that we have a list of medication prevalence, we can create a dataframe and sort by prevalence to determine which medications are most prevalent in our dataset.
In [26]:
medication_counts = pd.DataFrame({'medication': medications, 'prevalence':prevalence})
medication_counts = medication_counts.sort_values(by='prevalence', ascending=False)
medication_counts.head()
Out[26]:
| medication | prevalence | |
|---|---|---|
| 17 | insulin | 0.543779 |
| 0 | metformin | 0.229523 |
| 6 | glipizide | 0.138916 |
| 7 | glyburide | 0.118851 |
| 9 | pioglitazone | 0.082525 |
Let’s also visualize the top 10 most prevalent medications. We’ll use seaborn’s barplot method.
In [27]:
sns.barplot(x='medication', y='prevalence', data=medication_counts.head(10), palette='viridis')
plt.xticks(rotation=90)
plt.show()
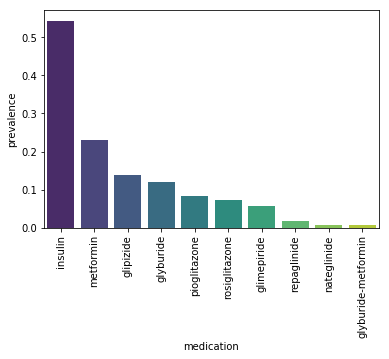
We can see that insulin is by far the most prevalent medication
followed by metformin. More than half of the patients in our dataset
were prescribed insulin whie 22% were prescribed metformin.
MeSH (or
Medical Subject Headings) are a type of “tag” that describes a medical
term. We’ll use RxNav’s API to further investigate which MeSH terms are
assocaited with our list of medications. We’ll cretea a function called
get_mesh_from_drug_name which returns relevant MeSH terms for a
given drug name.
In [28]:
import json
import requests
def get_mesh_from_drug_name(drug_name):
drug_name = drug_name.strip()
rxclass_list = []
try:
r = requests.get(f"https://rxnav.nlm.nih.gov/REST/rxclass/class/byDrugName.json?drugName={drug_name}&relaSource=MESH")
response = r.json()
all_concepts = response['rxclassDrugInfoList']['rxclassDrugInfo']
for i in all_concepts:
rxclass_list.append(i['rxclassMinConceptItem']['className'])
except:
pass
return list(set(rxclass_list))
We’ll pass the top 10 medications into get_mesh_from_drug_name and
get their relevant MeSH terms. The results will be stored in a
dictionary that we’ll call med_mesh_descriptors.
In [29]:
top_ten_meds = medication_counts.head(10)['medication'].tolist()
med_mesh_descriptors = dict()
for m in top_ten_meds:
med_mesh_descriptors[m] = get_mesh_from_drug_name(m)
In [30]:
med_mesh_descriptors
Out[30]:
{'insulin': [],
'metformin': ['Hypoglycemic Agents'],
'glipizide': ['Hypoglycemic Agents'],
'glyburide': ['Hypoglycemic Agents'],
'pioglitazone': ['Hypoglycemic Agents'],
'rosiglitazone': ['Hypoglycemic Agents'],
'glimepiride': ['Immunosuppressive Agents',
'Hypoglycemic Agents',
'Anti-Arrhythmia Agents'],
'repaglinide': ['Hypoglycemic Agents'],
'nateglinide': ['Hypoglycemic Agents'],
'glyburide-metformin': ['Hypoglycemic Agents']}
The results above show that all medications have the MeSH term
hypoglycemic
agent, which
means it’s an anti-diabetic medication. Interestingly, the medication
glimepiride also has two other associated MeSH terms
‘Anti-Arrhythmia Agents’ and ‘Immunosuppressive Agents’ in addition to
it being a hypoglycemic agent.
If you want to learn more about each medication in our dataset, check out the RxNav dashboard which gives an overview of medication properties and interactions.
Creating a Target Variable¶
The goal of our model will be to predict whether a patient will get
readmitted to the hospital. Looking at the readmitted column, we see
that there are 3 possible values:
NO(not readmitted)>30(readmitted more than 30 days after being discharged)<30(readmitted within 30 days of being discharged)
In [31]:
data['readmitted'].value_counts()
Out[31]:
NO 53212
>30 35545
<30 11357
Name: readmitted, dtype: int64
To keep things simple, we’ll view this as a binary classification
problem: did the patient get readmitted? We’re going to use
numpy.where to convert all instances of “NO” to 0 (means patient did
not get readmitted) and everyhting else to 1 (patient did get
readmitted).
In [32]:
data['readmitted_bool'] = np.where(data['readmitted']=='NO', 0, 1)
data['readmitted_bool'].value_counts()
Out[32]:
0 53212
1 46902
Name: readmitted_bool, dtype: int64
Step 4: Data Exploration and Visualization¶
Assessing Missing Values¶
To get a better sense of the missing values in our data, let’s visualize it using missingno’s “nullity” matrix.
In [33]:
import missingno as msno
msno.matrix(data)
Out[33]:
<matplotlib.axes._subplots.AxesSubplot at 0x1145977d0>

The data-dense columns are fully black, while the sparse columns (with missing values) have a mixture of white and black.
Patient Demographics: Age and Gender¶
In [34]:
plt.figure(figsize=(14,4))
plt.subplot(1,2,1)
sns.countplot(x='age', data=data, palette='viridis')
plt.title("Distribution of Age")
plt.subplot(1,2,2)
sns.countplot(data['gender'], palette='viridis')
plt.title("Distribution of Gender")
plt.show()
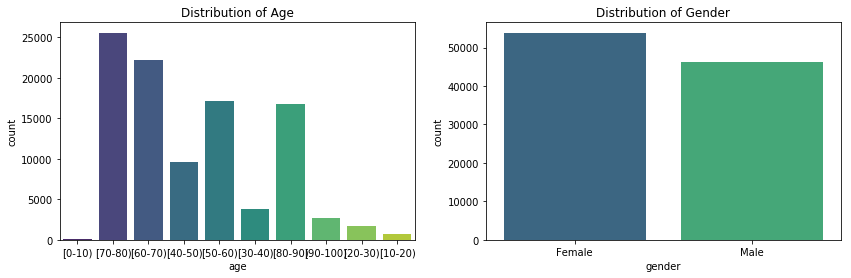
In [35]:
data['gender'].value_counts(normalize=True)
Out[35]:
Female 0.538013
Male 0.461987
Name: gender, dtype: float64
The age distribution plot shows that our dataset represents an aging population. The most common age range is 70-80 years old. Our population also has a higher proportion of females than males.
How long were hospital stays for a given admission?¶
In [36]:
plt.figure(figsize=(8,6))
sns.countplot(data['time_in_hospital'], palette='viridis')
plt.xlabel("time in hospital (days)")
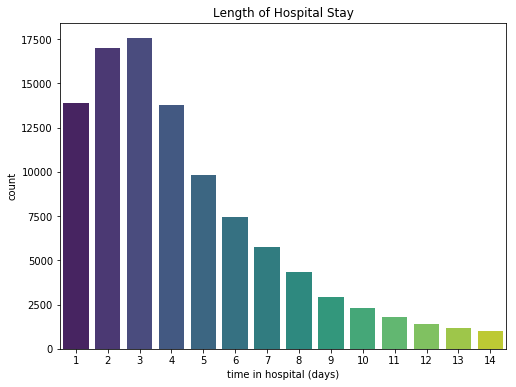
plt.title("Length of Hospital Stay")
plt.show()
In [37]:
print(f"Mean time in hospital: {data['time_in_hospital'].mean():.2f}")
Mean time in hospital: 4.39
Patients stayed on average 4.4 days in hospital. The longest stay was 14 days.
Number of Diagnoses, Procedures, Medications¶
In [38]:
plt.figure(figsize=(14,5))
plt.subplot(1,2,1)
sns.kdeplot(data['num_medications'], shade=True, legend=False)
plt.title(f"Number of Medications, mean: {data['num_medications'].mean():.2f}", size=14)
plt.subplot(1,2,2)
sns.kdeplot(data['num_lab_procedures'], shade=True, legend=False)
plt.title(f"Number of Lab Procedures, mean: {data['num_lab_procedures'].mean():.2f}", size=14)
plt.show()
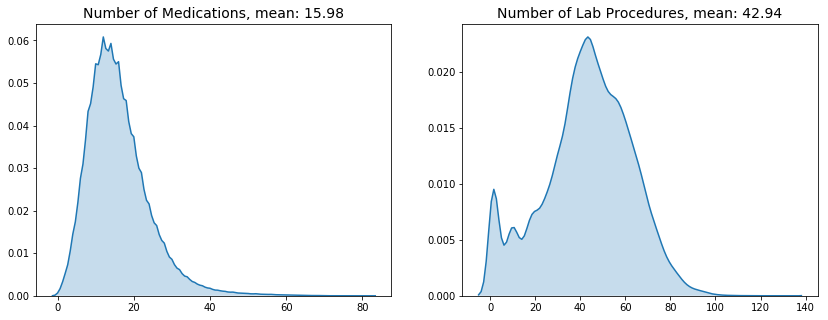
Patients on average were administered 16 medications during their hospital stay. The average number of lab procedures was 43.
What was the most common medical specialty?¶
We also have information on the medical specialty of a patient’s attending physician. This can give us a sense of the nature of a patient’s illness during their hospital stay. For example, “orthopedics” would suggest that the patient’s presenting issue was bone-related, while “nephrology” suggests a kidney problem.
In [39]:
medical_specialties = data['medical_specialty'].value_counts().reset_index()
medical_specialties.columns = ['specialty', 'count']
medical_specialties['prevalence'] = medical_specialties['count']/len(data)
print(f"There are {data['medical_specialty'].nunique()} medical specialties.")
medical_specialties.head(10)
There are 72 medical specialties.
Out[39]:
| specialty | count | prevalence | |
|---|---|---|---|
| 0 | InternalMedicine | 14328 | 0.143117 |
| 1 | Emergency/Trauma | 7449 | 0.074405 |
| 2 | Family/GeneralPractice | 7302 | 0.072937 |
| 3 | Cardiology | 5296 | 0.052900 |
| 4 | Surgery-General | 3068 | 0.030645 |
| 5 | Nephrology | 1544 | 0.015422 |
| 6 | Orthopedics | 1394 | 0.013924 |
| 7 | Orthopedics-Reconstructive | 1231 | 0.012296 |
| 8 | Radiologist | 1129 | 0.011277 |
| 9 | Pulmonology | 856 | 0.008550 |
What proportion of patients were on diabetes medication during their hospital stay?¶
In [40]:
data['diabetesMed'].value_counts(normalize=True)
Out[40]:
Yes 0.77184
No 0.22816
Name: diabetesMed, dtype: float64
77% of patients were on diabetes medication during their stay.
Do patients have normal A1C levels?¶
The A1C blood test is used to diagnose whether a patient has type I or II diabetes, and represents the average levels of blood sugar over the past 3 months. The higher the A1C level, the poorer a patient’s blood sugar control which indicates a higher risk of diabetes complications. The table below represents Mayo Clinic’s guideline of how to interpret A1C levels:
| interpretation | A1C level |
|---|---|
| no diabetes | <5.7 |
| pre-diabetes | 5.7-6.4 |
| diabetes | >6.5 |
| well-managed diabetes | <7 |
| poorly managed diabetes | >8 |
Our dataset has a A1Cresult which reflects a patient’s A1C level
during their hospital stay.
In [41]:
data['A1Cresult'].value_counts(normalize=True)
Out[41]:
>8 0.482994
Norm 0.292783
>7 0.224224
Name: A1Cresult, dtype: float64
In [42]:
print(f"Proportion of hospital admissions with missing A1C result: {data['A1Cresult'].isna().sum()/len(data):.2%}")
Proportion of hospital admissions with missing A1C result: 83.14%
Of the hospital admissions where A1C was measured, almost half had a A1C level of greater than 8, which suggests that the patient’s diabetes was poorly managed. However, the availability of A1C data is sparse in our dataset, so we may want to consider not including it in the first iteration of our model.
Step 5: Feature Selection and Engineering¶
Our dataset contains quite a few categorical variables such as race,
age, and admission_type. In general, machine learning models
can’t handle categorical variables so we can use one-hot and label
encoding to convert our string features to numerical without adding a
hierarchy.
One-hot Encoding¶
Let’s say we want to convert a patient’s race to a numerical feature. We could use label encoding to convert each race to values 0-5 but this suggests an inherent order among races that does not exist. With one-hot encoding, each race becomes an independent feature.
In [43]:
categorical = ['race', 'admission_type']
for c in categorical:
data = pd.concat([data, pd.get_dummies(data[c], prefix=c)], axis=1)
data.drop(columns=c)
In [44]:
data['age'].value_counts()
Out[44]:
[70-80) 25562
[60-70) 22185
[50-60) 17102
[80-90) 16706
[40-50) 9626
[30-40) 3765
[90-100) 2668
[20-30) 1650
[10-20) 690
[0-10) 160
Name: age, dtype: int64
Label Encoding¶
There are a couple of features where label encoding is applicable.
- age (from
[0-10)to[70-80)) can assume an ordinal relationship - gender (
MaleorFemale) converts to 0 and 1 which is binary
Let’s go ahead and apply scikit-learn’s LabelEncoder to these two columns.
In [45]:
from sklearn.preprocessing import LabelEncoder
label_encoder = LabelEncoder()
data['age_label'] = label_encoder.fit_transform(data['age'])
data['gender_bool'] = label_encoder.fit_transform(data['gender'].astype(str))
Because our gender column contained some missing values, it was
considered to be a mixed datatype. We had to convert it to a string
datatype in order to label encoding to work.
Data Modelling¶
Step 6: Defining the X and y Variables¶
Given that we now have a good understanding of our dataset, we can now
aim to build predictive models. The first step is to separate our
features and target into variables X and y respectively.
In [46]:
med_features = ['metformin_bool', 'repaglinide_bool',
'nateglinide_bool', 'chlorpropamide_bool', 'glimepiride_bool',
'acetohexamide_bool', 'glipizide_bool', 'glyburide_bool',
'tolbutamide_bool', 'pioglitazone_bool', 'rosiglitazone_bool',
'acarbose_bool', 'miglitol_bool', 'troglitazone_bool',
'tolazamide_bool', 'examide_bool', 'citoglipton_bool', 'insulin_bool',
'glyburide-metformin_bool', 'glipizide-metformin_bool',
'glimepiride-pioglitazone_bool', 'metformin-rosiglitazone_bool',
'metformin-pioglitazone_bool']
demographic_features = ['race_AfricanAmerican', 'race_Asian',
'race_Caucasian', 'race_Hispanic', 'race_Other', 'age_label',
'admission_type_Elective', 'admission_type_Newborn',
'admission_type_Trauma Center', 'admission_type_Urgent', 'gender_bool']
other_features = ['num_lab_procedures', 'num_procedures',
'num_medications', 'number_outpatient', 'number_emergency',
'number_inpatient', 'number_diagnoses']
all_features = med_features + demographic_features + other_features
X = data[all_features]
y = data['readmitted_bool']
Step 7: Choosing our Model¶
When building a binary classification model, there are a wide selection of machine learning models to choose from:
- Random Forest Classification
- Logistic Regression
- Linear Discriminant Analysis
- Support Vector Machines (SVM)
- Gaussian Naive Bayes
- k-Nearest Neighbours
We’ll test out the Random Forest Classifier (RFC) for this dataset. RFC is an ensemble learning technique that works by creating a “forest” of decision trees. Each tree evaluates the data for a given patient and outputs a 0 or 1. Random Forest looks at the output of all trees and gives the majority vote as its result. Let’s say we have a forest with 3 trees and 2 of them predict the patient will be readmitted. The majority vote is that the patient will be readmitted.
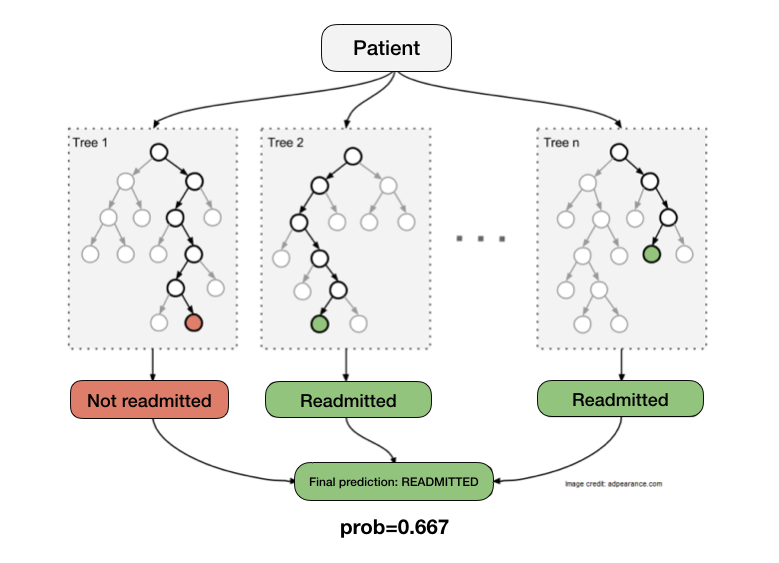
We’re choosing Random Forest because:
- it is robust to outliers
- it is able to handle unbalanced datasets
- it measures feature importance
We’ll import RFC from scikit-learn which is a very comprehensive Python library for data mining and data analysis.
In [47]:
from sklearn.ensemble import RandomForestClassifier
We can inspect the default parameters for RandomForestClassifier by
creating an instance of the class and applying get_params():
In [48]:
RandomForestClassifier().get_params()
Out[48]:
{'bootstrap': True,
'class_weight': None,
'criterion': 'gini',
'max_depth': None,
'max_features': 'auto',
'max_leaf_nodes': None,
'min_impurity_decrease': 0.0,
'min_impurity_split': None,
'min_samples_leaf': 1,
'min_samples_split': 2,
'min_weight_fraction_leaf': 0.0,
'n_estimators': 'warn',
'n_jobs': None,
'oob_score': False,
'random_state': None,
'verbose': 0,
'warm_start': False}
You can keep the default values for most of these parameters. But there are a few that can be modified prior to training the model that can impact model performance. These are called hyperparameters. Some RFC hyperparameters include:
n_estimators: number of trees in the forestmax_depth: maximum number of levels in each decision treemax_features: maximum number of features considered for splitting a nodemin_samples_split: number of data points placed in a node before the node is split
These are external configurations that can’t be learned from training the model. To select the optimal values of a hyperparameter, we’ll need to use a technique called hyperparameter tuning.
Step 8: Hyperparameter Tuning¶
Hyperparemter tuning is a critical step in the machine learning pipeline. It describes the process of choosing a set of optimal hyperparameters for a model. The hyperparameters that you select can have a significant impact on your model’s performance.
We’re going to be testing out two hyperparameter tuning techniques offered by scikit-learn:
With grid search, you define your search space as a grid of values and
iterate over each grid point until you find the optimal combination of
values. Let’s say we want to tune max_depth and n_estimators in
our RandomForestClassifer. We’ll set our search space as follows:
- n_estimators = [5,10,50]
- max_depth = [3,5,10]
This means that we’ll have to train our model 9 times to test for every configuration of values. We’ll choose the combination of n_estimators and max_depth that give us the best model performance.
Let’s implement this with scikit-learn’s GridSearchCV. We first need to define our search space as a dictionary. We also need to initialize our model.
In [49]:
from sklearn.model_selection import GridSearchCV
search_space = {
'n_estimators': [5,10,50],
'max_depth': [3,5,10]
}
rfc = RandomForestClassifier(random_state=42)
Now, we set up grid search. GridSearchCV also performs
cross-validation
(hence the 'CV') so we can specify how many folds we want in our
analysis. We’ll set our number of folds to 3. The more folds you use,
the longer it will take to compute results.
In [50]:
grid_search = GridSearchCV(rfc, search_space, cv=3)
The last step is to run fit. We’ll pass in X and y which we created in
Step 6. GridSearchCV will use RFC’s default metric,
accuracy.
If we want to optimize our model using another metric, we can specify
scoring = 'precision' (or whichever metric we’re interested in)
inside GridSearchCV. Let’s stick with accuracy for now.
In [51]:
grid_search.fit(X, y)
Out[51]:
GridSearchCV(cv=3, error_score='raise-deprecating',
estimator=RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators='warn', n_jobs=None,
oob_score=False, random_state=42, verbose=0, warm_start=False),
fit_params=None, iid='warn', n_jobs=None,
param_grid={'n_estimators': [5, 10, 50], 'max_depth': [3, 5, 10]},
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring=None, verbose=0)
What are the optimal hyperparameters?
In [52]:
print(f"Optimal hyperparameters: {grid_search.best_params_}")
print(f"Best score: {grid_search.best_score_:.3f}")
Optimal hyperparameters: {'max_depth': 5, 'n_estimators': 50}
Best score: 0.617
Based on the search space we defined for GridSearchCv, it looks like max_depth of 5 and n_estimators of 50 are our optimal hyperparmeters which gave us an accuracy of 0.617.
We can also see a thorough report of our results with cv_results_.
It shows fit time, score time, and mean train/test score (averaged over
all folds). We’ll sort by mean_test_score.
In [53]:
results = pd.DataFrame(grid_search.cv_results_).sort_values(by='mean_test_score', ascending=False)
results.head()
Out[53]:
| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_max_depth | param_n_estimators | params | split0_test_score | split1_test_score | split2_test_score | mean_test_score | std_test_score | rank_test_score | split0_train_score | split1_train_score | split2_train_score | mean_train_score | std_train_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 1.132375 | 0.009537 | 0.121620 | 0.001741 | 5 | 50 | {'max_depth': 5, 'n_estimators': 50} | 0.609014 | 0.633214 | 0.608373 | 0.616867 | 0.011562 | 1 | 0.633694 | 0.621683 | 0.627437 | 0.627605 | 0.004905 |
| 2 | 0.821872 | 0.007762 | 0.100330 | 0.000355 | 3 | 50 | {'max_depth': 3, 'n_estimators': 50} | 0.600264 | 0.627461 | 0.613047 | 0.613591 | 0.011110 | 2 | 0.624509 | 0.611839 | 0.619121 | 0.618490 | 0.005192 |
| 8 | 1.907094 | 0.071164 | 0.202362 | 0.028745 | 10 | 50 | {'max_depth': 10, 'n_estimators': 50} | 0.610332 | 0.621767 | 0.606814 | 0.612971 | 0.006383 | 3 | 0.655344 | 0.647828 | 0.647259 | 0.650144 | 0.003685 |
| 4 | 0.251050 | 0.008086 | 0.035588 | 0.000535 | 5 | 10 | {'max_depth': 5, 'n_estimators': 10} | 0.606107 | 0.624554 | 0.596686 | 0.609116 | 0.011574 | 4 | 0.631596 | 0.615375 | 0.622912 | 0.623294 | 0.006628 |
| 7 | 0.399570 | 0.004194 | 0.045592 | 0.000699 | 10 | 10 | {'max_depth': 10, 'n_estimators': 10} | 0.609553 | 0.614216 | 0.601510 | 0.608426 | 0.005248 | 5 | 0.654161 | 0.644068 | 0.642195 | 0.646808 | 0.005255 |
In 2012, Bergstra and Bengio from the University of Montreal proposed a new technique called random search which is similar to grid search but instead of sampling over a discrete set of values, you’re now randomly sampling from a distribution of values. Random search is effective in situations where not all hyperparameters are equally important.
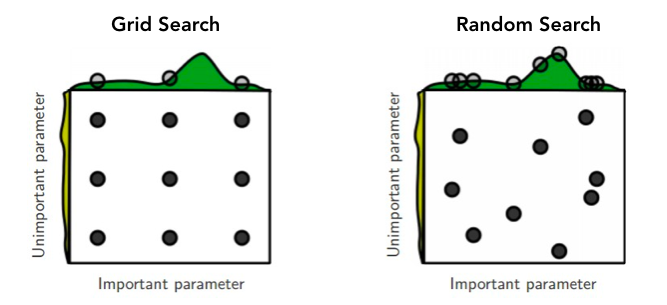
The visualization above gives an example of when random search can perform better. With grid search, you’re only looking at 3 different values of a given hyperparamter. But with random search you’re looking at nine different values. As you increase the number of samples in your random search, you increase the probability of finding the optimal hyperparameters for your model.
Let’s test out random search using scikit-learn’s RandomizedSearchCV. We’ll define our search space over a uniform distribution of values. We’ll iterate 9 times, just like we did for grid search.
In [54]:
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
search_space = {
"n_estimators": randint(10,100),
"max_depth": randint(1, 11)
}
random_search = RandomizedSearchCV(rfc, param_distributions=search_space, n_iter=9, cv=3)
random_search.fit(X,y)
print(f"Optimal hyperparameters: {random_search.best_params_}")
print(f"Best score: {random_search.best_score_:.3f}")
Optimal hyperparameters: {'max_depth': 4, 'n_estimators': 59}
Best score: 0.615
In [55]:
results = pd.DataFrame(random_search.cv_results_).sort_values(by='mean_test_score', ascending=False)
results.head()
Out[55]:
| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_max_depth | param_n_estimators | params | split0_test_score | split1_test_score | split2_test_score | mean_test_score | std_test_score | rank_test_score | split0_train_score | split1_train_score | split2_train_score | mean_train_score | std_train_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 1.149746 | 0.021392 | 0.129111 | 0.002811 | 4 | 59 | {'max_depth': 4, 'n_estimators': 59} | 0.606107 | 0.629858 | 0.609841 | 0.615269 | 0.010428 | 1 | 0.629873 | 0.614746 | 0.624890 | 0.623170 | 0.006294 |
| 0 | 1.136515 | 0.057328 | 0.126526 | 0.004007 | 4 | 58 | {'max_depth': 4, 'n_estimators': 58} | 0.605178 | 0.630068 | 0.609152 | 0.614799 | 0.010918 | 2 | 0.629634 | 0.614791 | 0.625174 | 0.623200 | 0.006218 |
| 1 | 2.200676 | 0.430752 | 0.166357 | 0.003467 | 6 | 65 | {'max_depth': 6, 'n_estimators': 65} | 0.609853 | 0.623895 | 0.609691 | 0.614479 | 0.006658 | 3 | 0.636511 | 0.625938 | 0.630029 | 0.630826 | 0.004353 |
| 6 | 2.004584 | 0.041066 | 0.205204 | 0.006243 | 6 | 80 | {'max_depth': 6, 'n_estimators': 80} | 0.610362 | 0.622247 | 0.608313 | 0.613640 | 0.006143 | 4 | 0.636661 | 0.626223 | 0.630313 | 0.631066 | 0.004294 |
| 4 | 2.834532 | 0.151390 | 0.263107 | 0.004990 | 9 | 77 | {'max_depth': 9, 'n_estimators': 77} | 0.610152 | 0.623925 | 0.606125 | 0.613401 | 0.007621 | 5 | 0.648422 | 0.641221 | 0.641520 | 0.643721 | 0.003326 |
Grid Search and Random Search are uninformed methods which means that they do not take into consideration results from past evaluations. When you’re working with a very large search space, you might want to consider a “smarter” approach to hyperparameter tuning such a Sequential-Based Model Optimization (SMBO). The SMBO approach keeps track of previous iteration results which is used to sample hyperapramters at the current iteration. In other words, SMBO is trying to reduce the number of iterations by sampling the most promising hyperparameters based on past results. You can check out scikit-optimize to learn more about how to implement SMBO hyperparameter tuning with scikit-learn models.
Step 9: Evaluating Model Performance¶
There are several metrics that we can use to evaluate model performance:
- accuracy
- precision
- recall
- F1-score
- ROC AUC score
A comprehensive list of classification metrics can be found in scikit-learn’s metrics module documentation.
In this walkthrough, we’ll look at accuracy, precision and recall. But before we can start evaluating our model, let’s split our data into two parts: 1) a training set and 2) a test set. We’ll fit our model on the training data, and evaluate its performance using the test set.
In [56]:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
rfc = RandomForestClassifier(**random_search.best_params_)
rfc.fit(X_train, y_train)
Out[56]:
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=4, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=59, n_jobs=None,
oob_score=False, random_state=99, verbose=0, warm_start=False)
Accuracy is RFC’s default evaluation metric. Using the score metric, we get the measured accuracy from the trained model.
In [57]:
accuracy = rfc.score(X_test, y_test)
print(f"Accuracy: {accuracy:.3f}")
Accuracy: 0.620
An accuracy score of 0.62 means that ~62% of hospital admissions were correctly labeled. The dataset that we’re working with is relatively balanced, but let’s say we have an imbalanced dataset where 90% of patients ended up being readmitted. Using accuracy to evaluate a model trained on imbalanced data is a problem because if we automatically predicted all patients to be readmitted, our accuracy would be 90% by default. Precision and recall are better ways to evaluate performance of models trained on imbalanced data.
Precision and Recall¶
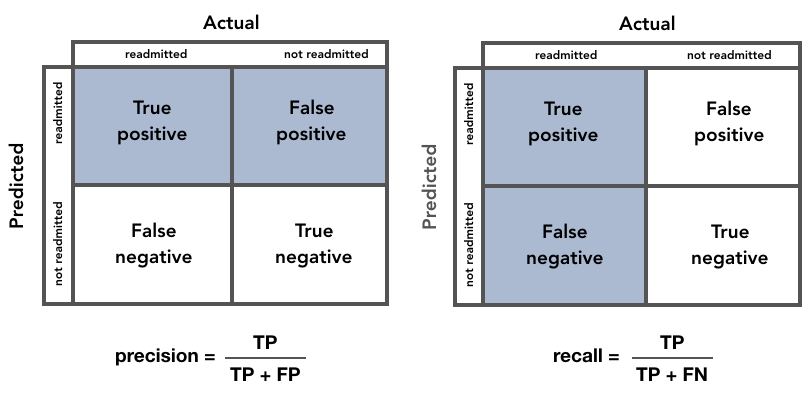
Precision and recall are information retrieval metrics that evaluate classification models.
- Precision
is the “fraction of relevant instances among the retrieved
instances”.
- What proportion of predicted readmitted patients were actually readmitted?
- Recall is the “fraction of the total amount of relevant instances
that were actually retrieved”.
- What proportion of readmitted patients were identified correctly?
Looking at the equations below, we can see that precision aims to minimize the number of False Positives, while recall aims to minimize the number of False Negatives.
In [58]:
from sklearn.metrics import precision_score, recall_score, confusion_matrix
y_pred = rfc.predict(X_test)
precision = precision_score(y_true=y_test, y_pred=y_pred)
recall = recall_score(y_true=y_test, y_pred=y_pred)
print(f"Precision: {precision:.3f}")
print(f"Recall: {recall:.3f}")
Precision: 0.621
Recall: 0.451
- Of the patients who were labelled as readmitted, ~62% were actually readmitted.
- Of the patients who were actually readmitted, 45% were labelled as readmitted.
Another way to assess our model’s performance is to visualize our results with a confusion matrix.
In [59]:
confusion = confusion_matrix(y_true=y_test, y_pred=y_pred)
labels = np.array([['TN','FP'],['FN','TP']])
sns.heatmap(confusion,annot=labels, fmt='', linewidths=2, cmap="Blues")
plt.xlabel("predicted")
plt.ylabel("actual")
Out[59]:
Text(33.0, 0.5, 'actual')
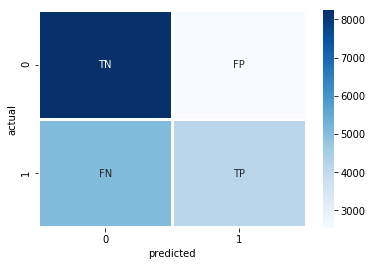
The heatmap above shows that we have more False Negatives than False Positives. This means that when we predict a patient will be readmitted, there’s a good chance that we got it right. But when we predict that a patient won’t be admitted, we’re missing quite a few patients who actually do return to the hospital.
Step 10: Examining Feature Importance¶
With RandomForestClassifier, we can dig further to examine which features were the most important in classification.
In [60]:
feature_importances = {
'features': list(X.columns.values),
'importance': list(rfc.feature_importances_)
}
important_features = pd.DataFrame(feature_importances)
important_features.sort_values(by='importance', ascending=False).head(15)
Out[60]:
| features | importance | |
|---|---|---|
| 39 | number_inpatient | 0.502475 |
| 38 | number_emergency | 0.145222 |
| 37 | number_outpatient | 0.103304 |
| 40 | number_diagnoses | 0.095260 |
| 36 | num_medications | 0.049601 |
| 28 | age_label | 0.021661 |
| 29 | admission_type_Elective | 0.019275 |
| 34 | num_lab_procedures | 0.018061 |
| 35 | num_procedures | 0.016270 |
| 17 | insulin_bool | 0.009118 |
| 0 | metformin_bool | 0.005045 |
| 25 | race_Caucasian | 0.003034 |
| 1 | repaglinide_bool | 0.001752 |
| 6 | glipizide_bool | 0.001735 |
| 24 | race_Asian | 0.001074 |
The most important feautures appear to be number_inpatient and
number_emergency, which represents the number of inpatient and
emergency visits of the patient in the year preceding the encounter. So
if a patient was admitted to the hospital in the past, this increases
their chance of being readmitted in the future.